Kreisberechnung: Kreis Umfang, Fläche, Formel
Was ist ein Kreis?
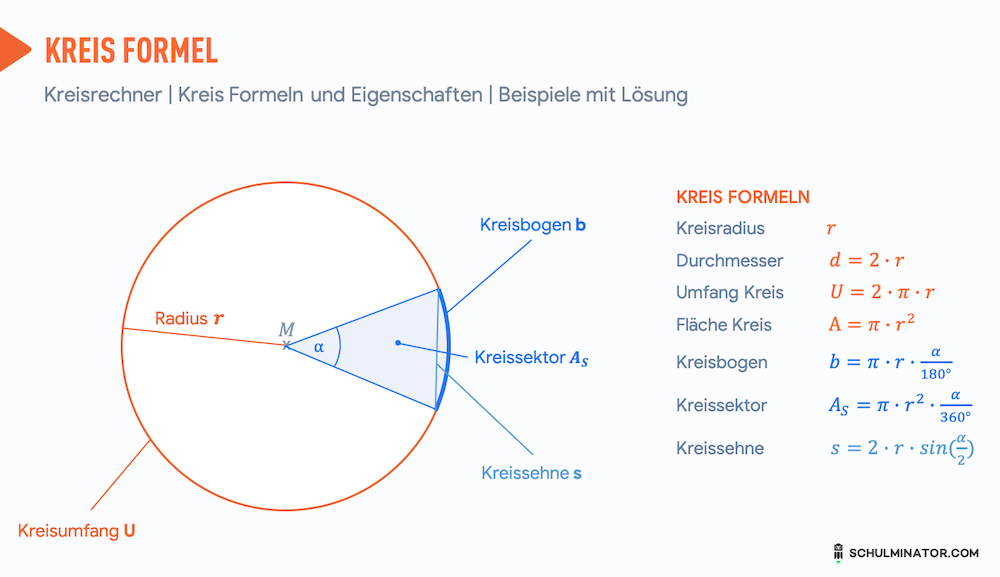
Ein Kreis ist eine geometrische Figur mit besonderen Eigenschaften:
- Alle Punkte auf einem Kreis haben den gleichen Abstand zum Mittelpunkt.
- Dieser konstante Abstand zwischen den Punkten auf dem Kreis und dem Mittelpunkt wird als Radius $r$ des Kreises definiert.
- Der Durchmesser des Kreises ist auch dessen Diagonale und ist doppelt so groß wie der Radius.
- Jede Gerade durch den Mittelpunkt eines Kreises bildet eine Symmetrieachse.
- Du kannst den Kreis beliebig um den Mittelpunkt drehen und es verändert sich nicht, damit ist der Kreis rotationssymetrisch.
Kreisbogen, Kreisausschnitt und Kreissehne
Man kann Ausschnitte aus dem Kreis berechnen. Diese ergeben sich, wenn zwei Radien eingezeichnet werden, um einen Winkel:
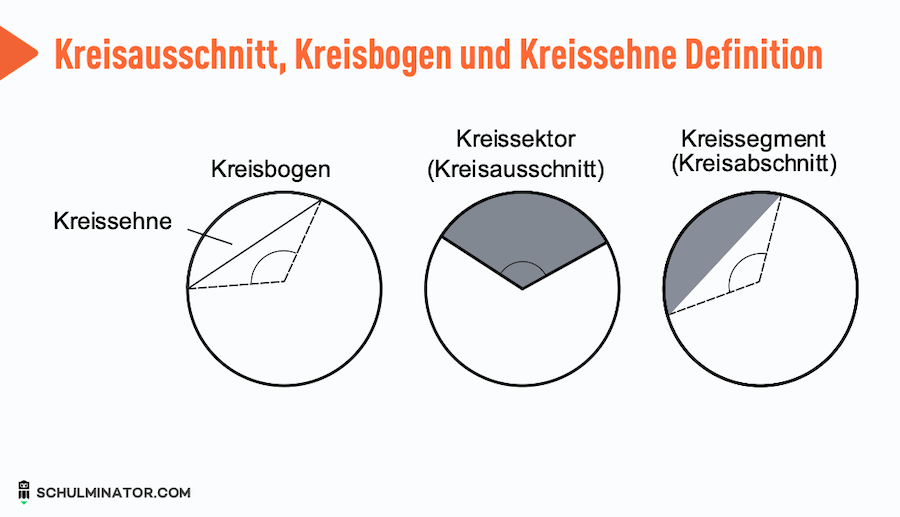
- Der Kreisausschnitt (auch Kreissektor) kann man sich wie ein Stück Pizza vorstellen. Es ist eine Fläche auf dem Kreis, das von 2 Radien mit einem bestimmten Winkel umspannt wird.
- Verbindet man zwei Punkte auf einem Kreis direkt miteinander, dann bezeichnet man diese Verbindungsstrecke als Kreissehne.
- Den Kreisbogen kannst Du dir vorstellen wie den Rand einer Pizza. Es ist die Verbindungslinie auf dem Kreis zwischen zwei Punkten (die direkte Verbindung ist die Kreissehne).
- Das Kreissegment (auch Kreisabschnitt) ist die Fläche zwischen dem Kreisbogen und der Kreissehne.
Kreis Aufgaben mit Lösungen
1. Kreisfläche und Kreisumfang berechnen
Berechne den Umfang und die Fläche der folgenden Rechtecke:
Der kreisförmige Teich von Onkel Messi hat einen Radius von $3m$. Messi will im Winter den Teich abdecken.
Wie groß muss die Fläche der Abdeckung sein?
Wie groß ist der Umfang der Abdeckung?
Für die Fläche der Abdeckung gilt:
$A = \pi \cdot r^2 = \pi \cdot 3^2 = 28,3m^2$
Ein Kreis hat den Umfang: $U = 2 \cdot \pi \cdot r = 2 \cdot \pi \cdot 3 = 18,9m$
Die Abdeckung muss mindestens eine Fläche von $0,716m^2$ haben und hat .
2. Kreisbogen und Kreisausschnitt berechnen
Berechne die Länge des Bogens $b$ und den Kreisausschnitt für $r=7cm$ und $\alpha = 70^\circ$.
Für den Kreisbogen gilt: $b = \pi \cdot r \cdot \frac{\alpha}{180^\circ} = \pi \cdot 7 \cdot \frac{70}{180^\circ} = 8,6cm$
Für den Kreisausschnitt gilt: $A_s = \pi \cdot r^2 \cdot \frac{\alpha}{360^\circ} = \pi \cdot 7^2 \cdot \frac{70}{360^\circ} = 30cm^2$
Kommentare
Einfach ausrechnen mit Online-Rechner 🪐
Weitere Lernmaterialien vom Autor 🦄
Top-Lernmaterialien aus der Community 🐬
Linien an Kreisen: Tangente, Sekante, Passante
Grundkonstruktionen: Mittelsenkrechte und Winkelhalbierende konstruieren







