Ereignis und Gegenereignis Erklärung und Beispiel

maria
12 Dezember 2022
#Wahrscheinlichkeitsrechnung
☆ 80% (Anzahl 2), Kommentare: 0
Erklärung

Definition Ereignis und Gegenereignis

  • Ein Ereignis $A,\,B,\,C,\,...$ ist eine bestimmte Teilmenge der Ergebnismenge $\Omega$ eines Zufallsexperiments.
  • Man schreibt dies mathematisch als $A\subset \Omega;\,B\subset \Omega;\,...$
  • Wenn das Ereignis als $A$ bezeichnet wird, wird das Gegenereignis als $\bar{A}$ bezeichnet.
  • Um zu einem Ereignis das Gegenereignis zu finden, kann man oft nach folgendem, einfachen Schema vorgehen:
    1. Ergebnismenge $\Omega$ bestimmen (z.B. anhand des Baumdiagramms)
    2. Ereignismenge $A$ bestimmen (z.B. durch abzählen)
    3. Die Gegenereignismenge ist die Restmenge oder Komplementärmenge $\bar{A}$.
  • Das Ereignis welches die gesamte Ergebnismenge $\Omega$ enthält $A=\Omega$ nennt man sicheres Ereignis.
  • Das Ereignis welches keine Elemente enthält bzw. das Nullelement, also $A=\{\}$ wird unmögliches Ereignis genannt.

 

 

Beispiele Ereignis und Gegenereignis

Beispiel 1

  • Eine Münze wird dreimal nacheinander geworfen.
  • über das Baumdiagramm findet man die Ergebnismenge $\Omega$ indem man jeden möglichen Pfad abläuft. ($Z$ = Zahl und $W$ = Wappen) $$\Omega=\{(ZZZ);(ZZW);(ZWZ);(ZWW);(WZZ);(WZW);(WWZ);(WWW)\}$$
  • Sei $A$ das Ereignis, das bei den drei Würfen mindestens 2 mal die Zahl geworfen wird. Wie lautet die Ereignismenge $A$?
    $A$ ist die Untermenge von $\Omega$, die mindestens 2 mal ein $Z$ enthält: $$A=\{(ZZZ);(ZZW);(ZWZ);(WZZ)\},\,Z\subset \Omega$$

 

Beispiel 2

  • Was sind die Gegenereignisse zu folgenden Ereignissen:
     
    Ereignis Gegenereignis
    A: Höchstens 4 Autos sind defekt. $\bar{A}$: Mindestens 5 Autos sind defekt.
    B: Mindestens 2 Handys wurden geklaut. $\bar{B}$: Höchstens ein Handy wurde gestohlen, d.h. keines oder eines.
    C: Kein Auto ist blau $\bar{C}$: Mindestens 1 Auto ist blau.
    D: Genau einer von drei äpfeln ist faul. $\bar{D}$: Keiner, zwei oder drei äpfel sind faul.

    Gehen wir bei Ereignis $A$ der Einfachheit halber von sechs Autos aus, können wir schreiben:

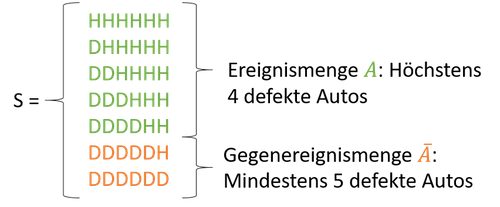
Baumdiagramm für einen zweimaligen Münzwurf
Baumdiagramm für einen zweimaligen Münzwurf

  • Wobei H einem heilen Auto entspricht und D einem defekten.
    Auf diese Art lassen sich die restlichen Gegenereignisse ebenso finden.
Wie hat dir dieses Lernmaterial gefallen?
Durchschnittliche Bewertung: 4 (Anzahl 2)

Kommentare