Was sind komplexe Zahlen?

Komplexe Zahlen $\mathbb{C}$ Definition

• Schon sehr einfache quadratische Gleichungen wie $$ x^2 + 1 = 0 $$ haben keine reelle Lösung mehr. Mit Hilfe der komplexen Zahlen läßt sich jedoch eine Lösung angeben: $$ x_1 = \sqrt{-1}, x_2 = -\sqrt{-1} $$ Für $\sqrt{-1}$ wählt man das Symbol $i$, und somit ist $i^2 = -1$. $i$ nennt man auch imaginäre Einheit.
• $z = a + bi$ mit $a, b \in \mathbb{R}$ heißt komplexe Zahl.
  $\bar{z} = a - bi$ heißt die zu $z$ konjugiert komplexe Zahl.
  Der Betrag von $z$ ist definiert durch $|z| = \sqrt{a^2 + b^2}$.
  $a$ heißt Realteil $(a = Re(z))$ und $b$ Imaginärteil $(b = Im(z))$.
• Zwei komplexe Zahlen sind gleich, wenn sie sowohl in Realteil als auch in Imaginärteil übereinstimmen: $$ a_1 + b_1i = a_2 + b_2i \Leftrightarrow a_1 = a_2 \wedge b_1 = b_2 $$
• Die Idee ist, den Zahlenstrahl wie bei den bisherigen Erweiterungen der natürlichen Zahlen, so zu erweitern, dass er mehr Zahlen darstellen kann. Der reelle Zahlenstrahl (eindimensional) lässt sich allerdings nicht mehr entlang seiner Achse erweitern, weshalb nur noch eine Erweiterung in die zweite Dimension bleibt.
• Zu diesem Zweck definieren wir einfach $i_2 := -1$, also $i = \sqrt{-1}$ und bezeichnen $i$ als die imaginäre Einheit. $i$ keine reelle Zahl.
• Eine komplexe Zahl besteht nun aus zwei Komponenten: Einem reellen Teil und einem komplexen Teil.
• Eine komplexe Zahl $z = a + ib$ lässt sich in einem zweidimensionalen Koordinatensystem darstellen. Auf der Re-Achse wird der reelle Anteil der Zahl abgetragen und auf der Im-Achse der imaginäre Teil.

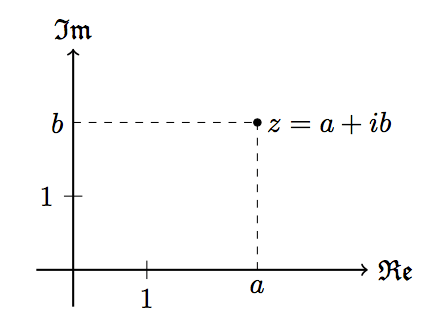
Komplexe Zahlen $\mathbb{C}$ Rechenregeln

• Mit komplexen Zahlen rechnet man wie mit reellen Zahlen. Somit ergibt sich für die Addition zweier komplexer Zahlen: $$ \begin{align} z_1 + z_2 &= (a_1 +b_1i)+(a_2 +b_2i) \\ &= (a_1 +a_2)+(b_1 +b_2)i \end{align} $$ 
• Analog ergibt sich für die Subtraktion: $$ \begin{aligned} z_1 -z_2 &= (a_2 +b_1i)-(a_2 +b_2i) \\ &= (a_1 -a_2)+(b_1 -b_2)i \end{aligned} $$
• Für die Multiplikation gilt nach den üblichen Rechenregeln für reelle Zahlen: $$ \begin{aligned} z_1 z_2 &= (a_1 + b_1i)(_a2 + b_2i) \\ &= a_1a_2 + a_1b_2i + b_1a_2i + b_1b_2i^2 \\ &= a_1a_2 + a_1b_2i + a_2b_1i − b_1b_2 \\ &= a_1a_2 - b_1b_2 + (a_1b_2 + a_2b_1)i \end{aligned} $$
• Um den Quotient zweier komplexer Zahlen zu berechnen, erweitert man den Bruch mit der konjugiert komplexen Zahl des Nenners: $$ \begin{aligned} \frac{z_1}{z_2} &= \frac{(a_1 + b_1i)(a_2 - b_2i)}{(a_2 + b_2i)(a_2 - b_2i)} \\ &= \frac{(a_1a_2 + b_1b_2) + (a_2b_1 - a_1b_2)i}{a^{2}_{2} + b^{2}_{2}} \end{aligned} $$

Komplexe Zahlen $\mathbb{C}$ Rechenregeln Beispiele

• Seien $z_1 = 2 - 3i$ und $z_2 = 3 + 2i$ zwei komplexe Zahlen.
• $\bar{z_1} =2+3i, \bar{z_2} =3-2i$
• $|z1|=\sqrt{2^2 + 3^2} =\sqrt{4+9}=\sqrt{13} \\ |z2|=\sqrt{3^2 +2^2} =\sqrt{13}$
• $z_1 + z_2 = (2-3i)+(3+2i) \\ = (2+3)+(-3+2)i = 5-i$
• $z_1 - z_2 =(2-3i)-(3+2i) \\ =(2-3)+(-3-2)i=-1-5i$
• $z_1 \cdot z_2 = (2 \cdot 3 - (-3) \cdot 2) + (2 \cdot 2+ (-3)\cdot 3)i \\ = (6+6)+(4-9)i = 12-5i$
• $$ \begin{aligned} \frac{z_1}{z_2} &= \frac{2 - 3i}{3 + 2i} \\ &= \frac{(2 - 3i)(3 - 2i)}{(3 + 2i)(3 - 2i)} \\ &= \frac{(2 \cdot 3 - (-3)(-2)) + (2 \cdot (-2) + (-3) \cdot 3)i}{3^2 + 2^2} \\ &= \frac{(6-6)+(-4-9)i}{13} = \frac{-13}{13}i = -i \end{aligned} $$

Die Gaußsche Zahlenebene

• Man kann komplexe Zahlen in der Ebene veranschaulichen, der Gaußschen Zahlenebene. Dabei trägt man den Realteil von $z$ auf der $x$-Achse und den Imaginärteil von $z$ auf der $y$-Achse auf. Die konjugiert komplexe Zahl $\bar{z}$ geht dann durch Spiegelung an der $x$-Achse aus der Zahl $z$ hervor.

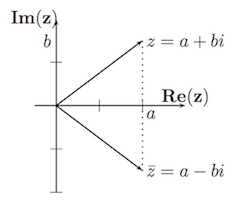
• Addition und Subtraktion komplexer Zahlen lassen sich mittels Vektoraddition graphisch darstellen

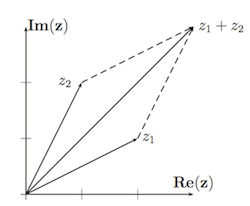
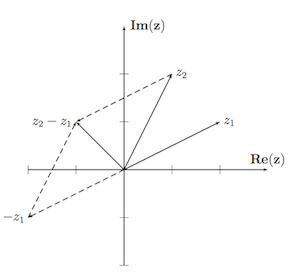
Polarkoordinatendarstellung der komplexen Zahlen $\mathbb{C}$

• Eine komplexe Zahl haben wir interpretiert als einen Punkt in der zweidimensionalen Ebene. Eine weitere Möglichkeit eine komplexe Zahl zu charakterisieren ist die sogenannte Polarform.
• In dieser Form wird die Länge des Zeigers $r$ und ein Winkel $0 \leq \varphi \leq 2\pi $ angegeben. Eine komplexe Zahl $z$ in Polarform ist dann gegeben durch $z = r(cos \varphi + i \cdot sin \varphi)$.

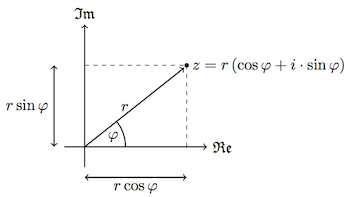
• Ist $z = a + bi$ so gilt für $r$ und $\varphi$:

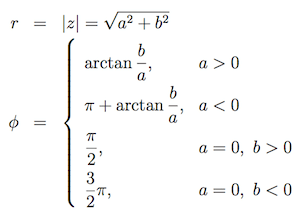
• $\varphi$ heißt auch Argument von $z (\varphi = arg(z))$ und ist bis auf Vielfache von $2\pi$ eindeutig bestimmt.
• Dies führt auf die sogenannte Polarkoordinatendarstellung der komplexen Zahlen: $$ z = a+bi = r(cos\varphi + isin\varphi) = re^{i\varphi} $$
• Mit Hilfe der Polarkoordinatendarstellung lässt sich die Multiplikation komplexer Zahlen in der Zahlenebene folgendermaßen berechnen: $$ \begin{aligned} z_1z_2 &= (r_1e^{i\varphi_1} )(r_2e^{i\varphi_2} ) \\ &= r_1(cos \varphi_1 + i sin \varphi_1)r_2(cos \varphi_2 + i sin \varphi_2) \\ &= r_1r_2(cos(\varphi_1 + \varphi_2) + i(sin(\varphi_1 + \varphi_2)) \\ &= r_1r_2ei(\varphi_1+\varphi_2) \end{aligned} $$ Für den Beweis werden die trigonometrischen Additionstheoreme oder die Potenzgesetze benötigt.