Sinussatz einfach erklärt: Formel, Beispiele, Aufgaben
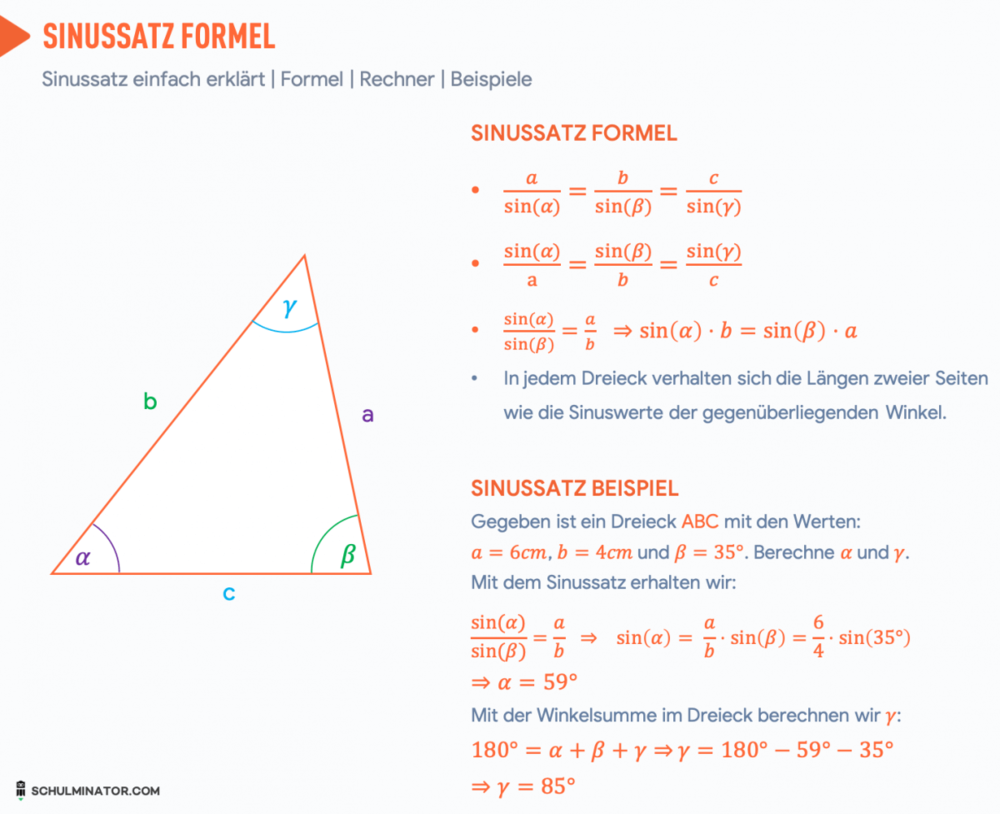
Was ist der Sinussatz? Sinussatz Formel und Erklärung
- In jedem Dreieck verhalten sich die Längen zweier Seiten wie die Sinuswerte der gegenüberliegenden Winkel:
- $ \frac {sin(\alpha)}{sin(\beta)} = \frac {a}{b} $ oder
- $ \frac {a}{sin(\alpha)} = \frac {b}{sin(\beta)} = \frac {c}{sin(\gamma)} $ oder $ \frac {sin(\alpha)}{a} = \frac {sin(\beta)}{b} = \frac {sin(\gamma)}{c} $
- Man kann den Sinussatz auch umstellen und wie folgt schreiben:
- $sin(\alpha) \cdot b = sin(\beta) \cdot a $
- Der Sinussatz setzt Winkel und Seiten in einem Dreieck in Beziehung zueinander. Damit kannst Du relativ einfach Winkel und Seitenlängen im Dreieck berechnen.
- Wenn in deinem Dreieck mindestens drei Größen gegeben mit einem Seiten-Winkel-Paar $ (a, \alpha), (b, \beta), (c, \gamma)$ enthalten ist, kannst du den Sinussatz verwenden, um die fehlenden Größen zu berechnen.
- Sind aber nur drei Seiten gegeben oder aber zwei Seiten und der eingeschlossene Winkel, dann musst du den Kosinussatz anwenden.
Sinussatz Aufgabe mit Lösung: Sinnussatz umstellen
Gegeben ist ein Dreieck $ABC$ mit folgenden Seiten- und Winkelgrößen:
$a=5,4cm$; $b=3,8cm$; $\alpha =73^{\circ }$
Berechne die fehlenden Winkel $\beta$ und $\gamma$, so wie die Seitenlänge $c$.
Winkel $ \beta $ berechnen:
Für die Berechnung des Winkels $\beta$ verwenden wir den Sinussatz:
$ \frac {a}{\sin \alpha } = \frac {b}{\sin \beta }$
jetzt den Sinussatz umstellen nach $\beta$:
$ \sin \beta = \frac {b\cdot \sin \alpha }{a} $ $= \frac {3,8cm \cdot \sin 73^{\circ}} {5,4cm} \approx 0,67$
Mit dem Arkussinus (Umkehrfunktion des Sinus) können wir den Winkel berechnen:
$ \beta \approx \arcsin(0{,}67)\approx 42^{\circ }$
Winkel $ \gamma $ berechnen:
Den Wert für $\gamma$ erhalten wir mit Hilfe der Winkelsumme im Dreieck (= alle Winkel ergeben 180°):
$\gamma =180^{\circ }-\alpha -\beta \approx 180^{\circ }-73^{\circ }-42^{\circ }=65^{\circ }$
Seitenlänge $ c $ berechnen:
Die Seitenlänge $ c$ berechnen wir mit dem Sinussatz und es gilt:
$ \frac {a}{\sin \alpha } = \frac {c}{\sin \gamma } $
Durch Umformung gelangt man so zum Ergebnis:
$ c=\frac {a\cdot \sin \gamma }{\sin \alpha } $ $\approx {\frac {5,4cm \cdot \sin 65^{\circ }}{\sin 73^{\circ }}} $ $\approx 5{,}1\,\mathrm {cm} $
Kommentare
Einfach ausrechnen mit Online-Rechner 🪐
Weitere Lernmaterialien vom Autor 🦄
Top-Lernmaterialien aus der Community 🐬
Kosinussatz einfach erklärt: Formel, Beispiel, Aufgaben
Trigonometrie Erklärung mit Formeln und Beispielen







