Mengenoperationen

Mengenoperationen

Vereinigung: $ A \cup B = \left\{x: x \in A \vee x \in B\right\} $

Durchschnitt: $ A \cap B = \left\{x: x \in A \wedge x \in B\right\} $

Differenz, Komplementärmenge: $ A \setminus B = \left\{x: x \in A \wedge x \notin B\right\} $

symmetrische Differenz: $ A \Delta B = (A \setminus B) \cup (B \setminus A) = (A \cup B) \setminus (A \cap B) $

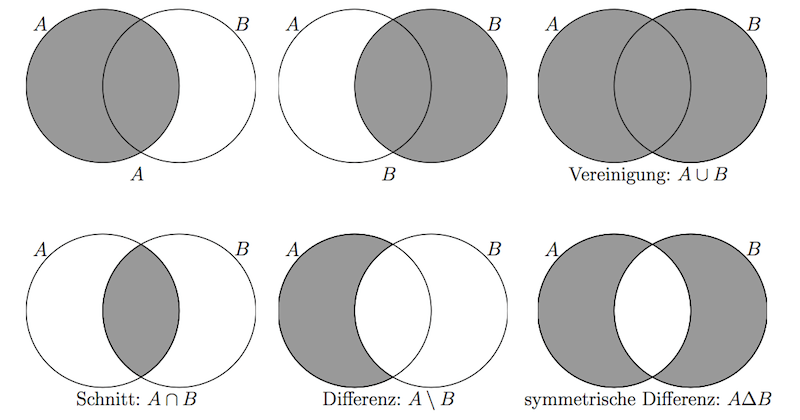
In der Abbildung sind die Mengenoperationen mit Hilfe sogenannter Venn-Diagramme illustriert.

Ist $ B \subset A $ fallen einige der Diagramme zusammen:

Für Mengenoperationen gelten die folgenden Regeln:

Assoziativgesetze $$ (A \cap B) \cap C = A \cap (B \cap C) \\ (A \cup B) \cup C = A \cup (B \cup C) $$

Kommutativgesetze $$ A \cap B = B \cap A \\ A \cup B = B \cup A $$

Morgansche Regeln $$ C \setminus (A \cap B) = (C \setminus A) \cap (C \setminus B) \\ C \setminus (A \cup B) = (C \setminus A) \cup (C \setminus B) $$

Distributivgesetze $$ (A \cap B) \cup C = (A \cup C) \cap (B \cup C)\\ (A \cup B) \cap C = (A \cap C) \cup (B \cap C) $$

Idempotenz $$ A \cap A = A, A \cup A = A $$

Diese Regeln entsprechen den Gesetzen für logische Operationen, wenn man die Operatoren $\cup,\cap$ durch $\vee,\wedge$ ersetzt und $\setminus$ durch $\neg$.

Beispiel