Änderungsrate, Differenzenquotient, Differenzialquotient Definition

Änderungsrate, Differenzenquotient, Differenzialquotient Definition

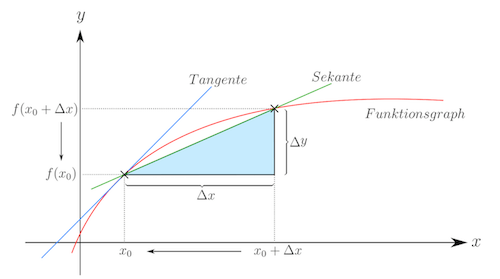
Die Sekantensteigungen gehen für $x_n \rightarrow \bar{x}$ in die Steigung der Tangente (und damit in die Ableitung) an der Stelle $\bar{x}$ über.

Die Änderung einer Funktion auf dem Intervall $[x; x_0 + \Delta x]$ ist: $f(x_0 +\Delta x) - f(x_0))$. 

Die durchschnittliche Änderung ist: $$ \frac{f(x_0 +\Delta x) - f(x_0)}{(x_0 + \Delta x) - x_0 } $$ Dies wird als Änderungsrate oder Differenzenquotient bezeichnet.

Differenzenquotient oder Änderungsrate einer Funktion

• Der Differenzenquotient einer Funktion $f$ in einem Intervall $[x; x_0 + \Delta x]$ ist gleich der Steigung der entsprechenden Sekante.
  Für die Sekantensteigung gilt: $$ \frac{f(x_0 +\Delta x) - f(x_0)}{(x_0 + \Delta x) - x_0 } = \frac{f(x_0 +\Delta x) - f(x_0)}{\Delta x} $$
• Der Differenzenquotient ist der Grenzwert des Differenzenquotienten für $\Delta x$ gegen Null.
  Ist f eine reelle Funktion, dann heißt der Grenzwert $$ \underset{x\rightarrow 0}{lim} = \frac{f(x_0 +\Delta x) - f(x_0)}{x_0}=f'(x) $$ Änderungsrate oder Differentialquotient von $f$ an der Stelle $x_0$.
• Wenn dieser Grenzwert existiert und für $ \Delta x \lt 0$ und $ \Delta x \gt 0$ gleich ist, so heißt die Funktion $f$ differenzierbar an der Stelle $x$. Die so erhaltene Funktion $f'$ nennt man Ableitung von $f$.
• Man kann sich unter dem Differentialquotienten an der Stelle $x$ näherungsweise einen Differenzenquotienten in einer sehr kleinen Umgebung von $x$ vorstellen.
• Mittlere Änderungsrate = Steigung der Sekanten = Differenzenquotient (Quotient aus Differenzen).
• Lokale Änderungsrate = Steigung der Tangenten = Differentialquotient (Grenzwert des Differenzenquotienten). Der Differentialquotient ist kein Quotient, sondern der Grenzwert eines Quotienten!

Die h-Methode zur Berechnung von Tangentensteigungen mit Beispielen