Eigenschaften von Folgen: Konvergenz und Divergenz

28 August 2020

☆ 60% (Anzahl 1), Kommentare: 0

Erklärung

Eine Zahl $g$ heißt Grenzwert der Zahlenfolge $(a_n)$ genau dann, wenn es zu jedem $\epsilon \gt 0$ einen Index $n_0$ gibt, so dass für alle $n \geq n_0$ gilt: $$ | a_n - g| \lt \epsilon $$

Schreibweise: $\underset{n \rightarrow \infty }{lim} a_n = g $

Besitzt eine Zahlenfolge einen Grenzwert $g$, so sagt man auch, die Folge konvergiert gegen den Grenzwert $g$.

Zu jeder (noch so kleinen) Zahl $\epsilon$ gibt es einen Index $n_0$, so dass alle Folgenglieder der Folge mit einem Index $n \geq n_0$ von dem Grenzwert $g$ einen kleineren Abstand als $\epsilon $ haben. Man sagt auch: Nur endlich viele Folgenglieder liegen außerhalb des "$\epsilon $-Schlauchs" um $g$.

Je kleiner man $\epsilon $ wählt, umso größer ist i.A. $n_0$ zu wählen, d.h. umso mehr Folgenglieder liegen außerhalb des $\epsilon $-Schlauchs. Wichtig ist nur: Ab einer Stelle liegen alle folgenden Glieder innerhalb des $\epsilon $-Schlauchs.

Eine Zahlenfolge kann höchstens einen Grenzwert haben.

Jede monoton wachsende (bzw. fallende) und gleichzeitig beschränkte Folge ist konvergent. Der Grenzwert entspricht der kleinsten oberen (größten unteren) Schranke der Folge.

Jede konvergente Zahlenfolge ist beschränkt. (Wie das Beispiel $(a_n) = ((-1)^n)$ zeigt, gilt die Umkehrung i.A. nicht.)

Jede Teilfolge einer gegen den Grenzwert $g$ konvergierenden Folge konvergiert ebenfalls gegen den Grenzwert $g$.

Eine Folge muss nicht konvergieren. So konvergiert beispielsweise die Folge $((-1)^n)$ nicht. Nicht-konvergente Zahlenfolgen heißen divergent.

Beispiel: Konvergenz und Divergenz

$n \longmapsto \frac{n}{n+1}, (a_n) = \frac{n}{n+1} = \left(\frac{1}{2}, \frac{2}{3}, \frac{3}{4},\frac{4}{5},...\right) $

Diese Folge nähert sich der Zahl 1 immer mehr an.

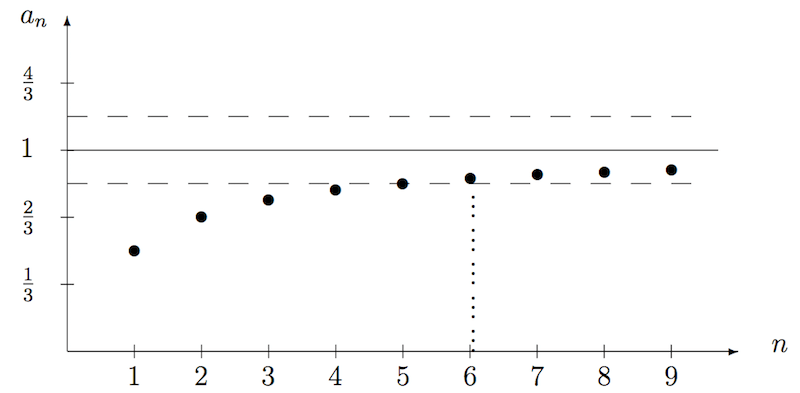
In der unteren Grafik sieht man, dass die Folge $(a_n) = \frac{n}{n+1}$ gegen den Wert 1 konvergiert. Wählt man wie in der graphischen Darstellung $\epsilon $ = 1, so liegen ab $n_0 = 6$ alle Folgenglieder innerhalb des "$\frac{1}{6}$-Schlauchs" um die Zahl 1.

Außerhalb des "$\frac{1}{6}$-Schlauches" findet man nur endlich viele Folgeglieder, nämlich die Glieder $a_1$ bis $a_5$.

Entsprechend ist für $\epsilon $ = $\frac{1}{1000}$ die Wahl $n_0 = 1000$ zu treffen, damit alle nachfolgenden Glieder innerhalb des "$\frac{1}{1000}$" -Schlauches um die Zahl 1 liegen.

Bild