Dreisatz einfach erklärt: Formel, Beispiele, Aufgaben
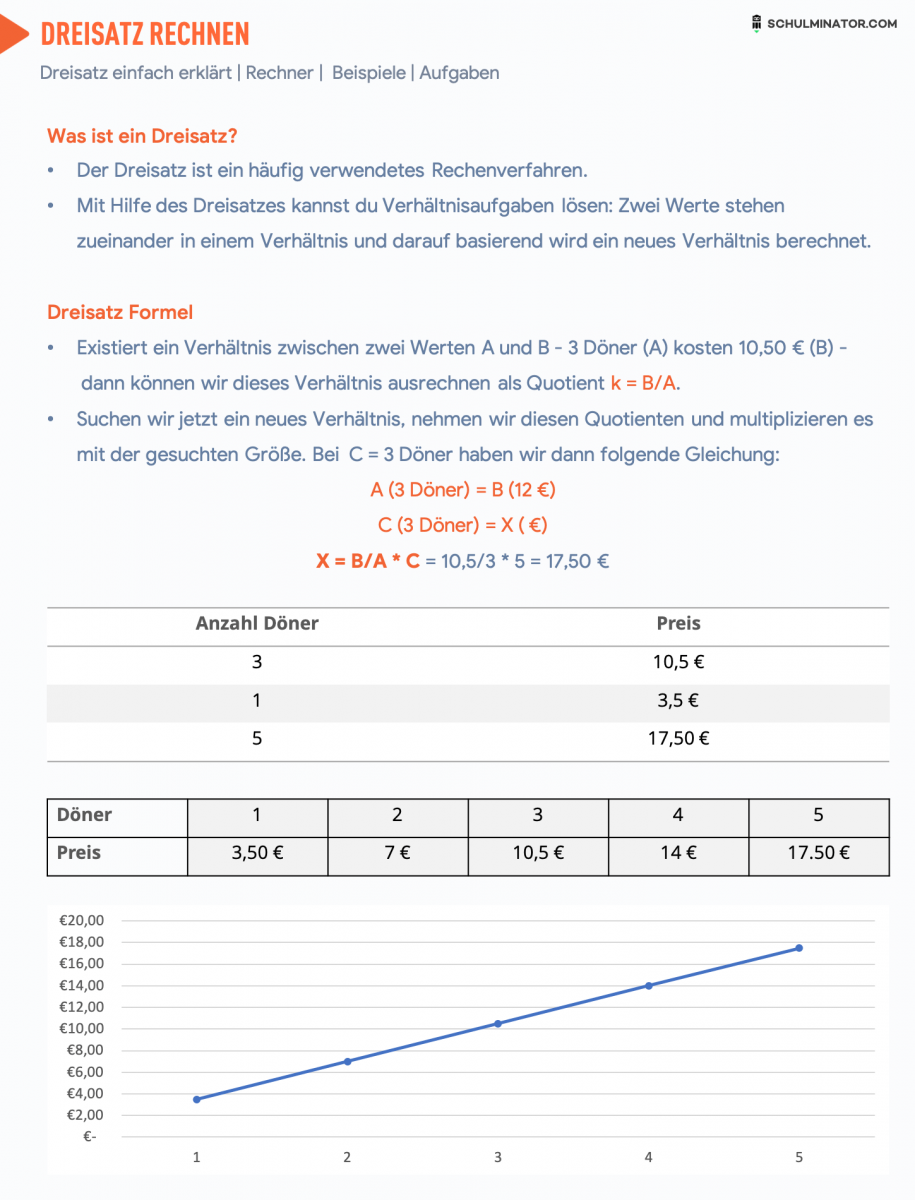
Was ist ein Dreisatz?
- Der Dreisatz ist ein häufig verwendetes Rechenverfahren.
- Mit Hilfe des Dreisatzes kannst du Verhältnisaufgaben lösen: Zwei Werte stehen zueinander in einem Verhältnis und darauf basierend wird ein neues Verhältnis berechnet.
- Mit dem Dreisatz lassen sich Aufgaben wie "2 kg Äpfel kosten 1,50 Euro, was kosten 3 kg?" bearbeiten.
- Die Bezeichnung "Dreisatz" kommt daher, dass die Aufgabe üblicherweise in drei Sätzen formuliert und bearbeitet wird.
Messi tankt für seinen Porsche $12l$ Benzin auf $60 km$. Wie viel schluckt das Auto auf $100$ km?
Schritt 1: Stelle das Verhältnis auf zwischen den beiden Werten
$60 km \triangleq 12l$
Schritt 2: Berechne den Verbrauch pro Einheit
$1 km \triangleq 12/60 = 0,2 l$
Schritt 3: Berechne den Verbrauch für die Menge
$100 km \triangleq 12/60 \cdot 100 = 0,2 \cdot100 = 20 l$
Dreisatz Aufgaben mit Lösung
Aufgabe 1: Benzinverbrauch beim Auto (proportionale Zuordnung)
Für eine Strecke von 240km benötigt ein Auto 18l Benzin.
1. Wie viel Benzin wird für 80km benötigt?
2. Wie weit kommt man mit dem Auto, wenn man nur 3l tankt?
Lösung 1:
$240km \triangleq 18l$
$1km \triangleq 18/240 \triangleq 0,075l$
$80km \triangleq 18/240 \cdot 80 = 0,075 \cdot 80 = 6l$
Lösung 2:
$240km \triangleq 18l$
$1l \triangleq 240/18 = 13,33km$
$3l \triangleq 240/18 \cdot 3 = 13,33 \cdot 3 = 39,99 km$
Aufgabe 2: Bananen bei Aldi (proportionale Zuordnung)
Beim Aldi kosten 4,5kg Bananen 6€.
1. Was kosten 2kg Bananen?
2. Wie viel kg Bananen bekommt man für 5€?
Lösung 1:
$4,5kg \triangleq 6€$
$1kg \triangleq 6/4,5 = 1,33€$
$2kg \triangleq 6/4,5 \cdot 2 = 1,33 \cdot 2 = 2,66€$
Lösung 2:
$4,5kg \triangleq 6€$
$1€ \triangleq 4,5/6 = 0,75kg$
$5€ \triangleq 4,5/6 \cdot 5 = 0,75 \cdot 5 = 3,75kg$
Aufgabe 3: Schwimmbecken auffüllen (antiproportionale Zuordnung)
Ein Schwimmbecken wird von 4 Pumpen in 14h gefüllt.
Wie schnell wird der Becken gefüllt, wenn 10 Pumpen eingesetzt werden?
Lösung:
$4 Pumpen \triangleq 14h$
$1 Pumpe \triangleq 14 \cdot 4 = 56h$ = benötigt alleine um das Becken zu füllen
$10 Pumpen$ benötigen $56h / 10 \triangleq 5,6h$
Dreisatz Formel
Wir können folgende Dreisatz Fomel aufstellen für die Aufgabe oben:
- Existiert ein Verhältnis zwischen zwei Werten $A$ und $B$, z.B. $3 Döner (A) \triangleq12 € (B)$, dann können wir dieses Verhältnis ausrechnen als Quotient $k = B/A$.
- Suchen wir jetzt ein neues Verhältnis, nehmen wir diesen Quotienten und multiplizieren es mit der gesuchten Größe. Bei $C = 3$ Döner haben wir dann folgende Gleichung:
$A$ (3 Döner) $\triangleq B$ (12 €)
$C$ (3 Döner) $\triangleq X$ (€)
$X \triangleq B/A \cdot C = $ 12€ / 3 Döner $\cdot$ 5 = 20 €
oder allgemeiner:
$A \triangleq B$
$C \triangleq X$
$X \triangleq B/A \cdot C$
Kommentare
Einfach ausrechnen mit Online-Rechner 🪐
Weitere Lernmaterialien vom Autor 🦄
Top-Lernmaterialien aus der Community 🐬
Proportionalität Übungen und Aufgaben mit Lösungen | PDF Download







