Prisma berechnen: Volumen, Fläche, Eigenschaften

Little Gauss

14 April 2023

#Geometrie, #Prisma

☆ 83% (Anzahl 6), Kommentare: 0

Bild

Erklärung

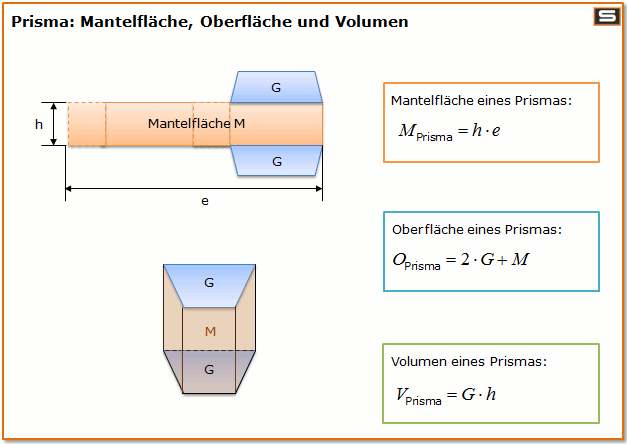
Prisma Formel: Volumen, Oberfläche, Mantelfläche

Die Grundfläche des Prismas bestimmt dessen Volumen:

$$ Volumen = Grundfläche \cdot Höhe $$

Grundfläche Dreieck: $G = \frac{1}{2}g \cdot h$

Grundfläche Parallelogramm: $G = a \cdot h_a$

Grundfläche Trapez: $G = \frac{a+c}{2}g \cdot h$

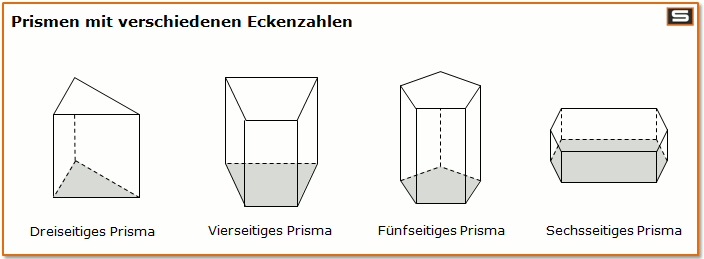
Was ist ein Prisma? Dreisitige und mehrseitige Prismen

Ein Prisma ist ein geometrischer Körper mit besonderen Eigenschaften: Grundfläche und Deckfläche sind parallel zueinander und sind deckungsgleiche Vielecke.
Die Eckzahl der Grundfläche von Prismen bestimmt dessen Benennung.
Die Grundfläche und die Deckfläche sind parallel zueinander und sind Vielecke.
Ein Zylinder ist kein Prisma, da die Grundfläche kreisförmig ist und nicht ein Vieleck.
Eine Pyramide ist auch kein Prisma, da es zur Grundfläche gibt es keine deckungsgleiche und parallele Deckfläche.

Lehrer Uwe hat heute im Physik-Unterricht ein vierseitiges Prisma vorgestellt. Er nimmt Maß und stellt fest, dass die Grundfläche $32cm^2$ beträgt und $12cm$ hoch ist.

Ali träumt vor sich hin und überlegt sich, wie viel Schokolade er wohl bräuchte, um das Prisma damit komplett aufzufüllen.

Eine 100g Tafel Schokolade hat die Maße: $8cm$, $16cm$, $1cm$.

Für das Volumen des Prismas gilt:

$ V_{Prisma} = G \cdot h = 32cm^2 \cdot 12cm = 384cm^3 $

Die Schokolade hat ein Volumen von $ V_{Schokolade} = 8 \cdot 16 \cdot 1 = 128cm^3 $.

Anzahl der benötigten Tafeln: $ 384 \div 128 = 3 $.

Um sein Traum zu verwirklichen braucht Ali 3 Tafeln Schokolade.

Bild