Kegelstumpf berechnen: Volumen, Mantelfläche, Oberfläche

mathepanda
29 Januar 2023
#Kegel, #Kegelstumpf
☆ 80% (Anzahl 13), Kommentare: 0
Bild
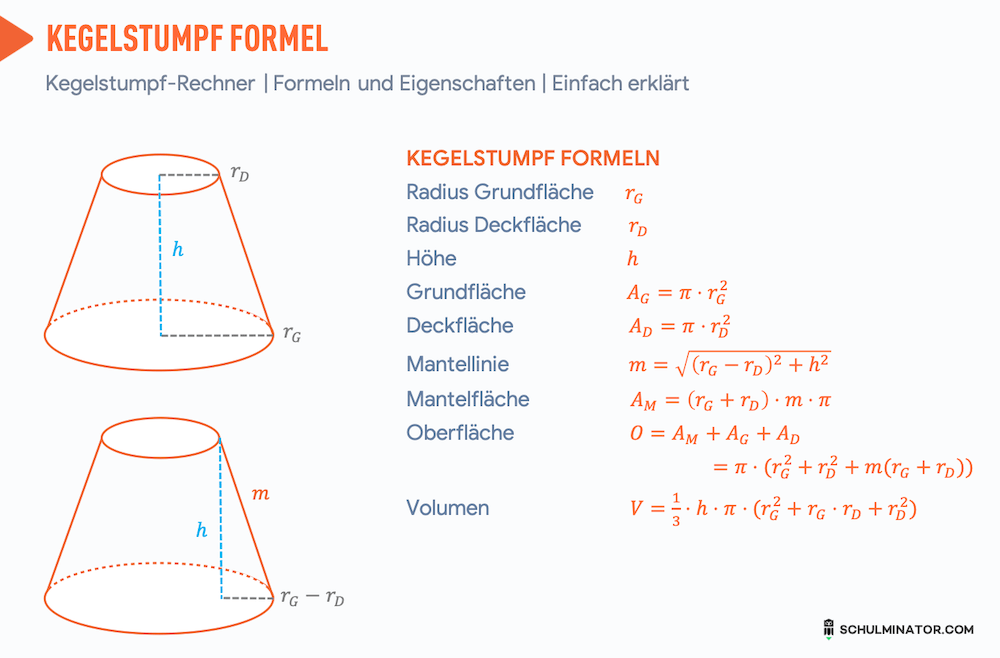
Kegelstumpf Formel: Mantelfläche, Deckfläche, Oberfläche, Volumen
Erklärung

Was ist ein Kegelstumpf? Kegelstumpf Eigenschaften

  • Ein Kegelstumpf ist ein Kegel, bei dem die Spitze abgeschitten wurde.
  • Die größere der beiden parallelen Kreisflächen wird als Grundfläche bezeichnet und die kleinere Fläche wird als Deckfläche bezeichnet.
  • Die Mantelfläche ist die Kegelstumpffläche ohne die beiden Kreisflächen.
  • Die Höhe des Kegels ist definiert als der Abstand zwischen Grundfläche und Deckfläche.

  

Kegelstumpf Aufgabe mit Lösung: Volumen und Mantelfläche berechnen

Gegeben ist ein Kegelstumpf mit Grundflächenradius $r_G = 20cm$ und Deckflächenradius $r_D = 10cm$. Die Höhe beträgt $h=10cm$.

Berechne das Volumen und die Mantelfläche des Kugels.

Für die Mantelfläche gilt:

$A_M = (r_G+r_D) \cdot m \cdot \pi = (20 + 10) \cdot 10 \cdot \pi = 1332,8 cm^2$

Das Volumen des Kegelstumpfs wird berechnet mit der folgenden Formel:

$ V = \frac{1}{3} \cdot h \cdot  \pi \cdot (r_G^2 + r_G \cdot r_D + r_D^2) $

$ V = \frac{1}{3} \cdot 10 \cdot  \pi \cdot (20^2 + 20 \cdot 10 + 10^2) = 7330,4 cm^3 $

Wie hat dir dieses Lernmaterial gefallen?
Durchschnittliche Bewertung: 4 (Anzahl 13)

Kommentare