Lineare Gleichungssysteme lösen: Additionsverfahren, Substitutionsverfahren, Gleichsetzungsverfahren
☆ 83% (Anzahl 8), Kommentare: 0
Erklärung
Definition lineare Gleichungssysteme
- Unter einem linearen Gleichungssystem versteht man 2 lineare Gleichungen mit zwei Variablen.
- Eine Lösung des linearen Gleichungssystems sind alle Zahlenpaare, die beide Gleichungen erfüllen. Die Menge der Lösungen bezeichnet man als Lösungsmenge.
- Das Ziel der verschiedenen Lösungsverfahren – Additions-, Einsetzungs- und Gleichsetzungsverfahren – ist es aus zwei Gleichungen mit zwei Unbekannten eine Gleichung mit einer Unbekannten herzustellen.
Bild

Erklärung
Additionsverfahren Erklärung
- Das Ziel des Additionsverfahrens ist es die Gleichungen so umzuformen, dass bei der Addition der beiden Gleichungen eines der Variablen wegfällt.
- Die beiden Gleichungen können auch voneinander subtrahiert werden.
- Besonders sinnvoll ist das Additionsverfahren, wenn die Koeffizienten einer Variablen in den zwei Gleichungen zueinander entgegengesetzte Zahlen sind.
Bild

Erklärung
Substitutionsverfahren oder Einsetzungsverfahren Erklärung
- Beim Einsetzungsverfahren löst man eine der Gleichungen nach einer Variablen auf (x oder y) und setzt diese Variable dann in die andere Gleichung ein.
- Besonders sinnvoll ist das Einsetzungsverfahren, wenn bereits eine der beiden Gleichungen nach einer Variablen aufgelöst ist.
Bild

Erklärung
Gleichsetzungsverfahren Erklärung
- Beim Gleichsetzungsverfahren löst man beide Gleichungen nach derselben Variablen und setzt diese dann gleich.
- Das Gleichsetzungsverfahren ist ein Sonderfall des Einsetzungsverfahrens, und zwar wenn bereits beide Gleichungen nach einer Variablen aufgelöst sind.
- Es eignet sich besonders, wenn beide Gleichungen nach der gleichen Variable aufgelöst vorliegen.
Bild

Erklärung
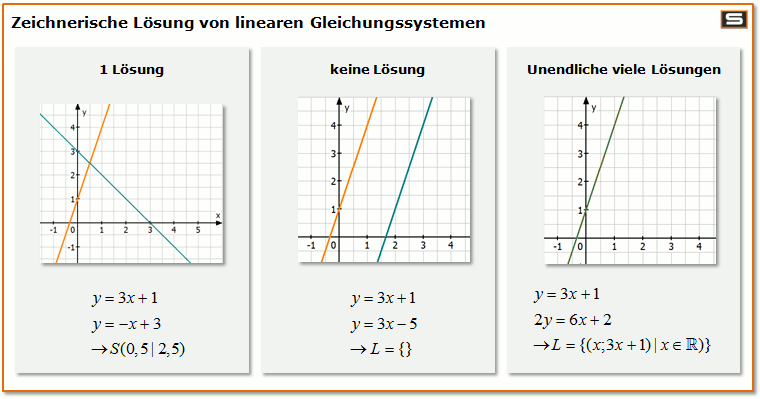
Zeichnerische Lösung
- Man kann ein lineares Gleichungssystem auch grafisch lösen, da beide Gleichungen eine Gerade bzw. eine lineare Funktion darstellen.
- Bringe die beiden Gleichungen in die Geradenform: y=mx+c.
- Wenn sich die Geraden in einem Punkt S (x|y) schneiden, dann ist das genau die eine Lösung des Gleichungssystems.
- Schneiden sich die Geraden nicht, also sind sie parallel zueinander, dann gibt es keine Lösung.
- Liegen beide Geraden übereinander, dann gibt es unendlich viele Lösungen, d. h. jedes beliebige Wertepaar x und y ist eine Lösung für das Gleichungssystem.
Bild
Wie hat dir dieses Lernmaterial gefallen?
Kommentare
Top-Lernmaterialien aus der Community 🐬
Lineare Gleichungssysteme Aufgaben mit Lösungen | PDF Download
☆ 76% (Anzahl 10), Kommentare: 0






