Quadratische Funktionen Erklärung und Scheitelpunktform berechnen
☆ 76% (Anzahl 5), Kommentare: 0
Bild

Bild
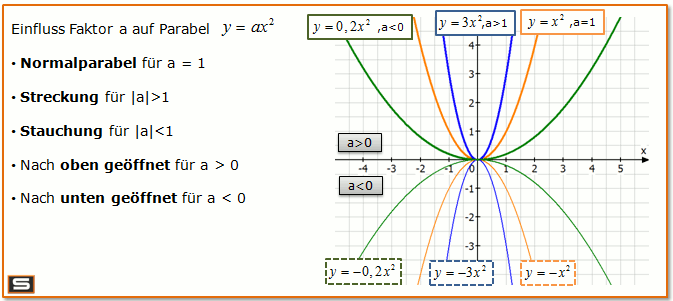
Bild
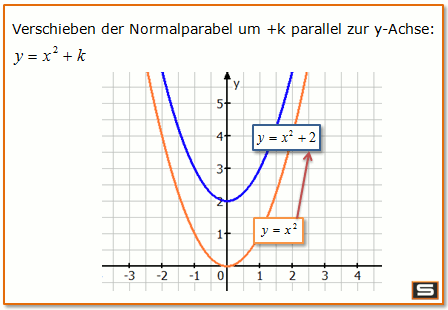
Bild

Bild
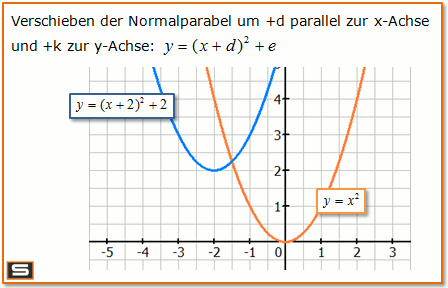
Bild

Bild
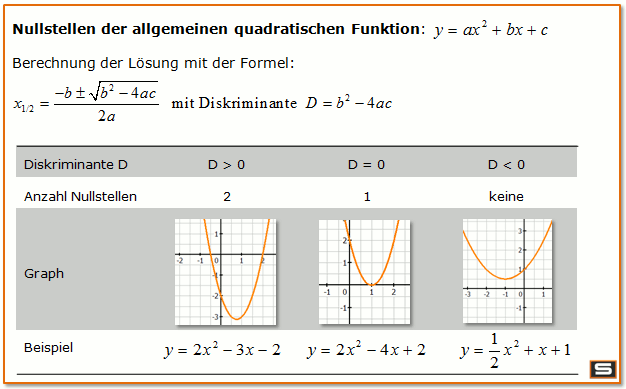
Wie hat dir dieses Lernmaterial gefallen?
Kommentare
Top-Lernmaterialien aus der Community 🐬
☆ 60% (Anzahl 1), Kommentare: 0
Lineare Funktionen Erklärung: Steigungsdreieck, y-Achsenabschnitt
☆ 92% (Anzahl 12), Kommentare: 0
Einführung Funktionen Arbeitsblatt und Aufgaben mit Lösungen | PDF Download
☆ 75% (Anzahl 4), Kommentare: 0






