Rechteck berechnen: Flächeninhalt, Umfang, Diagonale

19 März 2024

☆ 64% (Anzahl 11), Kommentare: 0

Bild

Erklärung

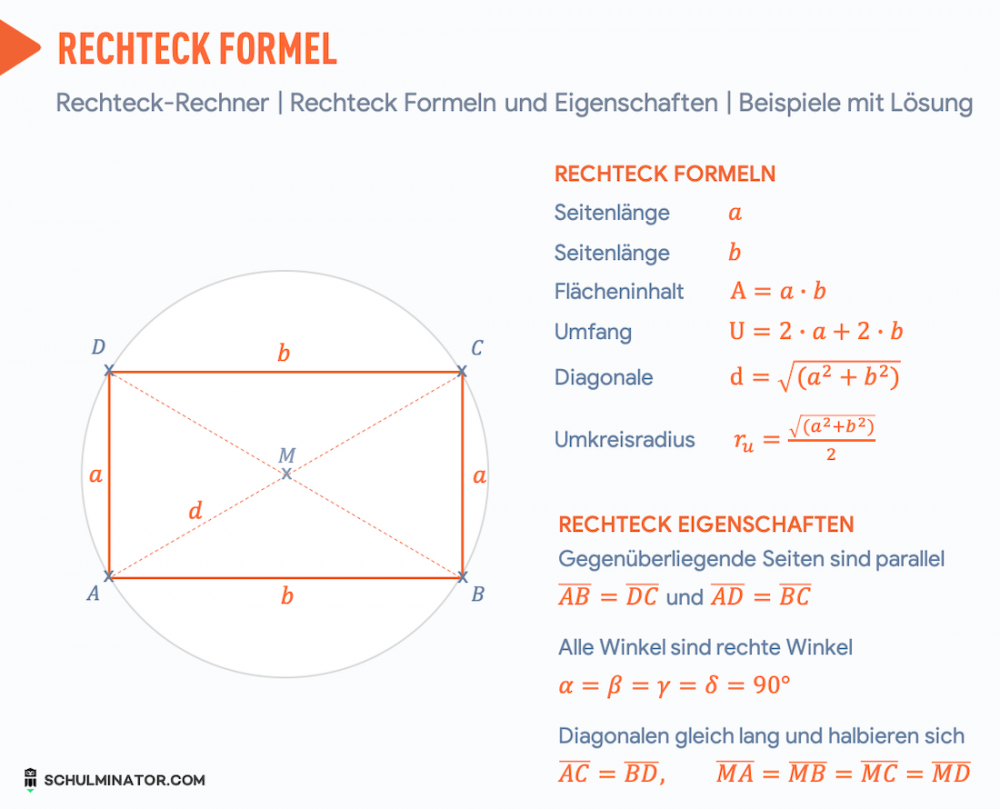
Was ist ein Rechteck? Rechteck Eigenschaften

Ein Rechteck ist ein spezielles Viereck mit den folgenden Eigenschaften:

Die gegenüberliegenden Seiten sind gleich lang: $\overline{AB} = \overline{DC}$ und $ \overline{AD} = \overline{BC}$
Die gegenüberliegenden Seiten sind parallel zueinander: $AB \parallel DC, AD \parallel BC$
Die vier Winkel im Rechteck sind rechte Winkel - alle Winkel sind 90°: $\alpha = \beta = \gamma = \delta = 90^\circ$
Die Diagonalen sind gleich lang: $\overline{AC} = \overline{BD}$
Die Diagonalen halbieren sich gegenseitig: $\overline{MA} = \overline{MB} = \overline{MC} = \overline{MD}$

Jedes Quadrat ist auch ein Rechteck, nämlich eines mit lauter gleich langen Seiten.
Seiten: Beim Rechteck sind jeweils nur die gegenüberliegenden Seiten gleich lang, aber nicht alle Seiten.
Diagonalen: Beim Quadrat schneiden sich die Diagonalen senkrecht, aber nicht beim Rechteck. Sowohl beim Rechteck als auch beim Quadrat, sind die Diagonalen gleich lang und halbieren sich.

Berechne den Umfang und die Fläche der folgenden Rechtecke:

A) $a=4cm, b=3cm$

B) $a=14cm, b=2,5cm$

C) $a=3,5m, b=8m$

Die Rechtecke haben die folgenden Flächen:

A) $a=4cm$, $A=a \cdot b = 4cm \cdot 3cm = 12cm^2$

B) $a=14cm$, $A=a \cdot b = 14cm \cdot 2,5cm = 35cm^2$

C) $a=3,5m$, $A=a \cdot b = 3,5m \cdot 8m = 28m^2$

Bei den folgenden Rechtecken ist nur die Fläche $A$ gegeben und die Seitenlänge $a$. Berechne die Seitenlänge $b$ und den Umfang:

A) $A=30cm^2, a=5cm$

B) $A=80km^2, a=10km$

Die Rechtecke haben die folgenden Seitenlänge und den Umfang:

A) $A= a \cdot b$ damit ist $b = \frac{A}{a} = \frac{30cm^2}{5cm} = 6cm$
Der Umfang berechnet sich wie folgt: $U= 2a + 2b = 10cm + 12cm = 24cm$

B) Für b gilt: $b = \frac{A}{a} = \frac{80km^2}{10km} = 8km$
Der Umfang ist damit: $U= 2a + 2b = 20km + 16km = 36km$

Lukaku bekommt zum Geburtstag eine Tafel Schokolade geschenkt. Mit einem Lineal misst er folgende Werte:
$a=15cm$ und $b=10cm$.

Er fragt sich nun:

Er möchte die Schokolade in einer großen Kugel verstecken, die er später basteln möchte.

Lukaku erinnert sich an die Rechteck Formel und kann damit die Fläche der Tafel Schokolade berechnen:

Die Diagonale der Tafel kann er mit der Formel für die Diagonale berechnen:

$d = \sqrt{a^2 + b^2} = \sqrt{(15)^2 + (10)^2} = \sqrt{(15)^2 + (10)^2} = \sqrt{225 + 100} $
$d = \sqrt{225 + 100} = \sqrt{325} = 18cm$
Die Diagonale der Tafel Schokolade ist 18cm.
Die oben berechnete Diagonale entspricht dem mindest Durchmesser der Kugel. Hätte die Kugel einen kleineren Durchmesser, dann würde die Tafel Schokolade nicht mehr hinein passen.

Wie hat dir dieses Lernmaterial gefallen?