Mehrstufige Zufallsexperimente und Pfadregeln Erklärung und Beispiel
☆ 92% (Anzahl 5), Kommentare: 0
Erklärung
Definition: Mehrstufige Zufallsexperimente und Pfadregeln
- Mehrstufige Zufallsexperimente sind Zufallsexperimente, die in zwei oder mehreren Schritten nacheinander durchgeführt werden.
- Beim berechnen der Wahrscheinlichkeit mithilfe des Baumdiagramms kann die Pfadregel verwendet werden.
- Die Pfadregel besteht aus der Produkt- und Summenregel
- Die Wahrscheinlichkeit eines einzelnen Pfades berechnet sich durch Multiplikation der einzelnen Wahrscheinlichkeiten entlang des Pfades (Produktregel).
- Gehören zu einem Ereignis mehrere Pfade des Baumdiagramms, so berechnet man die Wahrscheinlichkeit für das Ereignis, indem man die Wahrscheinlichkeiten der einzelnen Pfade addiert (Summenregel).
Beispiel: Mehrstufige Zufallsexperimente und Pfadregeln
Werden zwei gezinkte Münzen mit $p(\mathrm{Zahl})=0,6$ nacheinander geworfen, so gehören zum Ereignis $E$: "unterschiedliche Seiten liegen oben" zwei Pfade im Baumdiagram.
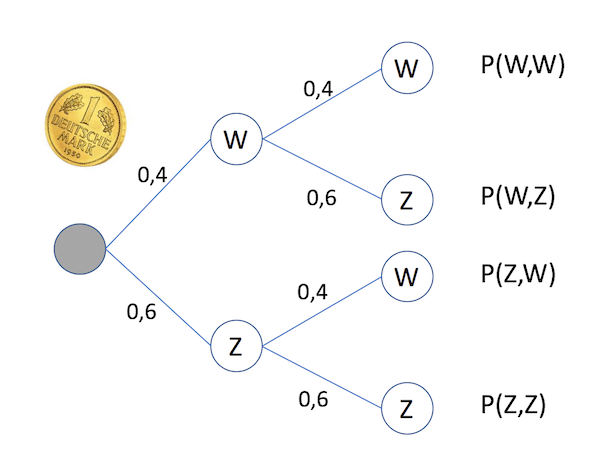
Die Wahrscheinlichkeit für $E$ folgt nach der Pfadregel zu: $$ p(E)=p(WZ \cup ZW) \\ =p(WZ)+p(ZW) \\ = 0,4\cdot0,6+0,6\cdot0,4 =0,48 $$
Wie hat dir dieses Lernmaterial gefallen?
Kommentare
Weitere Lernmaterialien vom Autor 🦄
Top-Lernmaterialien aus der Community 🐬
Kombinatorik Erklärung mit Formeln, Beispielen und Aufgaben
☆ 63% (Anzahl 43), Kommentare: 0
Geordnete Stichprobe ohne Zurücklegen Definition und Beispiel
☆ 73% (Anzahl 6), Kommentare: 0
Vierfeldertafel Erklärung mit Beispiel
☆ 67% (Anzahl 3), Kommentare: 0





