Bedingte Wahrscheinlichkeit Erklärung mit Beispielen
Bedingte Wahrscheinlichkeit Definition
- Wenn zwei Ereignisse nicht unabhängig sind, können wir also durch das Eintreten des einen Ereignisses etwas über das andere aussagen (oder "lernen").
- Dies führt zum Konzept der bedingten Wahrscheinlichkeiten (auch konditionale Wahrscheinlichkeit). Diese treten zum Beispiel dann auf, wenn ein Zufallsexperiment aus verschiedenen Stufen besteht und man sukzessive das Resultat der entsprechenden Stufen erfährt.
- Bedingte Wahrscheinlichkeit ist die Wahrscheinlichkeit des Eintretens eines Ereignisses $A$ unter der Bedingung, dass das Eintreten eines anderen Ereignisses $B$ bereits bekannt ist.
- Die bedingte Wahrscheinlichkeit von $A$ gegeben $B$ ist definiert als $$ P(A|B) = \frac{P(A \cap B)}{P(B)} $$ Die Interpretation ist folgendermassen: $P (A | B)$ ist die Wahrscheinlichkeit für das Ereignis $A$, wenn wir wissen, dass das Ereignis $B$ schon eingetroffen ist.
- Die bedingte Wahrscheinlichkeit kann also als Neueinschätzung der Wahrscheinlichkeit von $A$ interpretiert werden, wenn die Information vorliegt, dass das Ereignis $B$ bereits eingetreten ist.
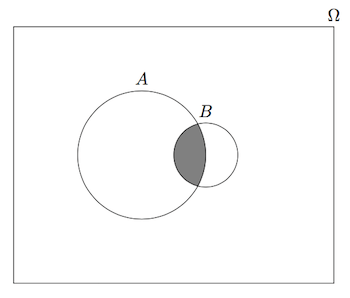
- Wie kann man die Formel verstehen? Da wir wissen, dass $B$ schon eingetreten ist (wir haben also einen neuen Grundraum $\Omega' = B$), müssen wir von $A$ nur noch denjenigen Teil anschauen, der sich in $B$ abspielt (daher $A \cap B$). Dies müssen wir jetzt noch in Relation zur Wahrscheinlichkeit von $B$ bringen: die Normierung mit $P(B)$ sorgt gerade dafür, dass $P (\Omega') = P (B) = 1$.
- Dies ist auch in der Abbildung oben illustriert. Wenn man wieder mit Flächen denkt, dann ist die bedingte Wahrscheinlichkeit $P (A | B)$ der Anteil der schraffierten Fläche an der Fläche von $B$.
Bedingte Wahrscheinlichkeit Beispiele: Würfel
Was ist die Wahrscheinlichkeit, eine 6 zu würfeln? Offensichtlich 1/6! Was ist die Wahrscheinlichkeit, eine 6 zu haben, wenn wir wissen, dass eine gerade Zahl gewürfelt wurde?
Wir haben hier: $$ \Omega = \left\{1,...,6\right\} , A = \left\{6\right\} \textrm{ und } B = \left\{2,4,6\right\} $$ Durch die zusätzliche Information (gerade Augenzahl) hat sich die Wahrscheinlichkeit für eine 6 also geändert.
Bedingte Wahrscheinlichkeit Beispiele: Vereinstreffen
Zu einem deutsch-französischen Vereinstreffen erscheinen 80 Franzosen und 120 Deutsche. 60% der deutschen Teilnehmer sind blond, dagegen nur 20% der französischen.
Mit welcher Wahrscheinlichkeit ist:
a) ein blonder Teilnehmer ein Franzose
b) ein nicht-blonder Teilnehmer ein Deutscher
c) ein nicht-blonder Teilnehmer ein Franzose
a) $P_{blond} (Franzose) = \frac{0,4 \cdot 0,2}{0,4 \cdot 0,2 + 0,6 \cdot 0,6} = 18,2% $
b) $P_{nicht blond} (Deutscher) \frac{0,6 \cdot 0,4}{0,6 \cdot 0,4 + 0,4 \cdot 0,8} = 42,9% $
c) $P_{nicht blond} (Franzose) \frac{0,4 \cdot 0,8 }{0,6 \cdot 0,4 + 0,4 \cdot 0,8} = 57,1% $
Bedingte Wahrscheinlichkeit Rechenregeln
- $0 \leq P (A | B) \leq 1$ für jedes Ereignis A
- $P (B | B) = 1$
- $P(A_1 \cup A_2 |B)= P(A_1|B) + P(A_2|B)$ für $A_1$, $A_2$ disjunkt (d.h. $A_1 \cap A_2 = \emptyset $)
- $P(A^c|B) = 1 - P(A|B)$ für jedes Ereignis $A$
- So lange man am "bedingenden Ereignis" B nichts ändert, kann man also mit bedingten Wahrscheinlichkeiten wie gewohnt rechnen. Sobald man aber das bedingende Ereignis ändert, muss man sehr vorsichtig sein (siehe unten).
- Weiter gilt für zwei Ereignisse $A$, $B$ mit $P (A) \gt 0$ und $P (B) \gt 0$: $$ P (A \cap B) = P (A | B) P (B) = P (B | A) P (A) $$ Deshalb können wir die Unabhängigkeit auch folgendermassen definieren: $$ A,B \textrm{ unabhängig } \Leftrightarrow P(A | B) = P(A) \Leftrightarrow P(B | A) = P(B) $$
- Unabhängigkeit von $A$ und $B$ bedeutet also, dass sich die Wahrscheinlichkeiten nicht ändern, wenn wir wissen, dass das andere Ereignis schon eingetreten ist. Oder nochmals: "Wir können nichts von $A$ über $B$ lernen" (bzw. umgekehrt).
- Oft werden im Zusammenhang mit bedingten Wahrscheinlichkeiten falsche Rechenregeln verwendet und damit falsche Schlussfolgerungen gezogen. Man beachte, dass im Allgemeinfall $$ P (A | B) \neq P (B | A) P (A | B^c) \neq 1 - P (A | B) $$ Man kann also bedingte Wahrscheinlichkeiten in der Regel nicht einfach "umkehren" (erste Gleichung). Dies ist auch gut in der Abbildung oben ersichtlich. $P (A | B)$ ist dort viel grösser als $P (B | A)$.
Kommentare
Top-Lernmaterialien aus der Community 🐬
Geordnete Stichprobe mit Zurücklegen Erklärung mit Beispiel
Bedingte Wahrscheinlichkeit Aufgaben mit Lösungen | PDF Download
Satz von Bayes Definition und Beispiele







