Satz des Thales einfach erklärt: Defintion, Beweis, Aufgaben

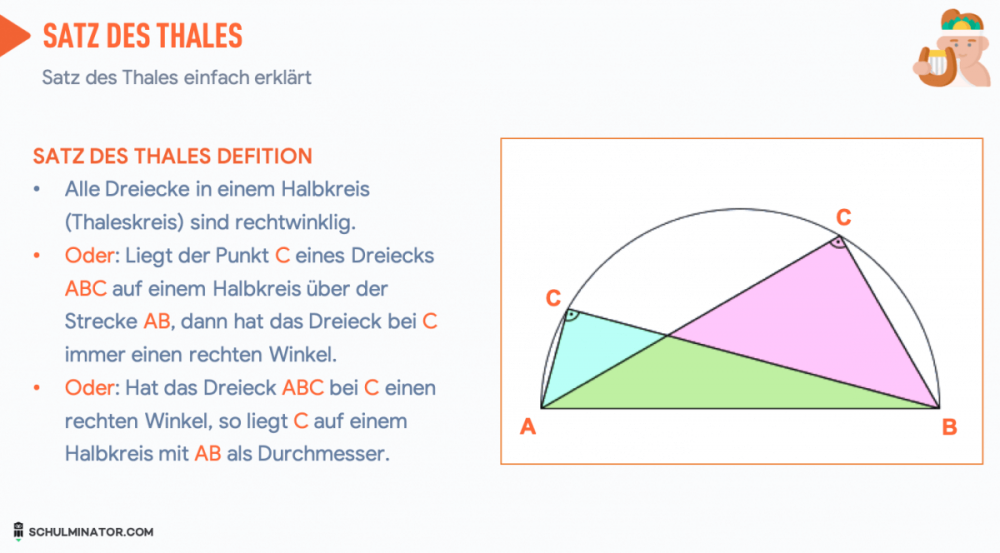
Satz des Thales Definition

Der Satz des Thales ist eines der ältesten Sätze der Mathematik (ca. 600 v. Chr.) und damit noch älter als der Satz des Pythagoras. Der Satz ist benannt nach dem griechischen Mathematiker und Philosophen Thales von Milet (624 – 547 v. Chr.).

Oder: Liegt der Punkt C eines Dreiecks ABC auf einem Halbkreis über der Strecke AB, dann hat das Dreieck bei C immer einen rechten Winkel.

Oder: Hat das Dreieck ABC bei C einen rechten Winkel, so liegt C auf einem Halbkreis mit AB als Durchmesser.

Satz des Thales Aufgabe mit Lösung

Satz des Thales Beweis

Um den Satz des Thales zu beweisen gelten folgende zwei Aussagen: 

• In jedem gleichschenkligen Dreieck sind die Winkel an der Basis gleich.
• Die Winkelsumme im Dreieck ist 180°.

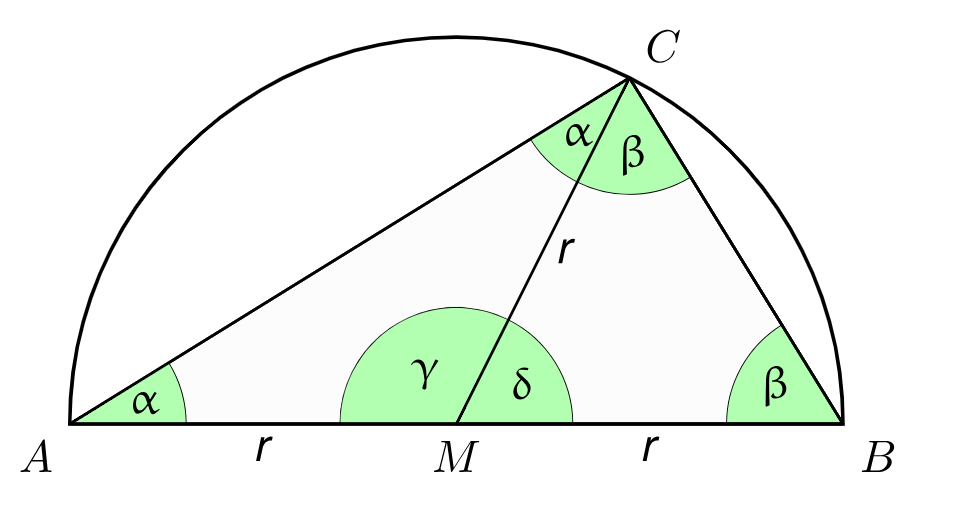
ABC sei ein Dreieck innerhalb eines Kreises mit [AB] als Kreisdurchmesser und dem Radius r. Dann ist der Mittelpunkt M der Strecke [AB] auch der Kreismittelpunkt. Die Streckenlängen [AM], [BM] und [CM] sind also gleich dem Radius r.

Die Strecke [CM] teilt das Dreieck ABC in zwei Dreiecke AMC und BCM auf, die gleichschenklig sind. Die Basiswinkel dieser Dreiecke, also die Winkel an der Grundseite [AC] bzw. [BC], sind daher jeweils gleich $\alpha $ beziehungsweise $ \beta $in der Abbildung).

Die Winkelsumme im Dreieck ABC beträgt 180°:

• $ \alpha +\beta +\alpha +\beta \,=\,180^{\circ } $
• $ 2(\alpha +\beta )\,=\,180^{\circ }  $

Dividiert man diese Gleichung auf beiden Seiten durch 2, so ergibt sich:

• $ \alpha +\beta \,=\,90^{\circ } $

Damit ist gezeigt, dass der Winkel  $ \alpha +\beta $  mit Scheitel C ein rechter Winkel ist.