Drachenviereck berechnen: Flächeninhalt, Formel, Eigenschaften

mathepanda
12 September 2024
#Drache, #Viereck
☆ 46% (Anzahl 26), Kommentare: 0
Erklärung

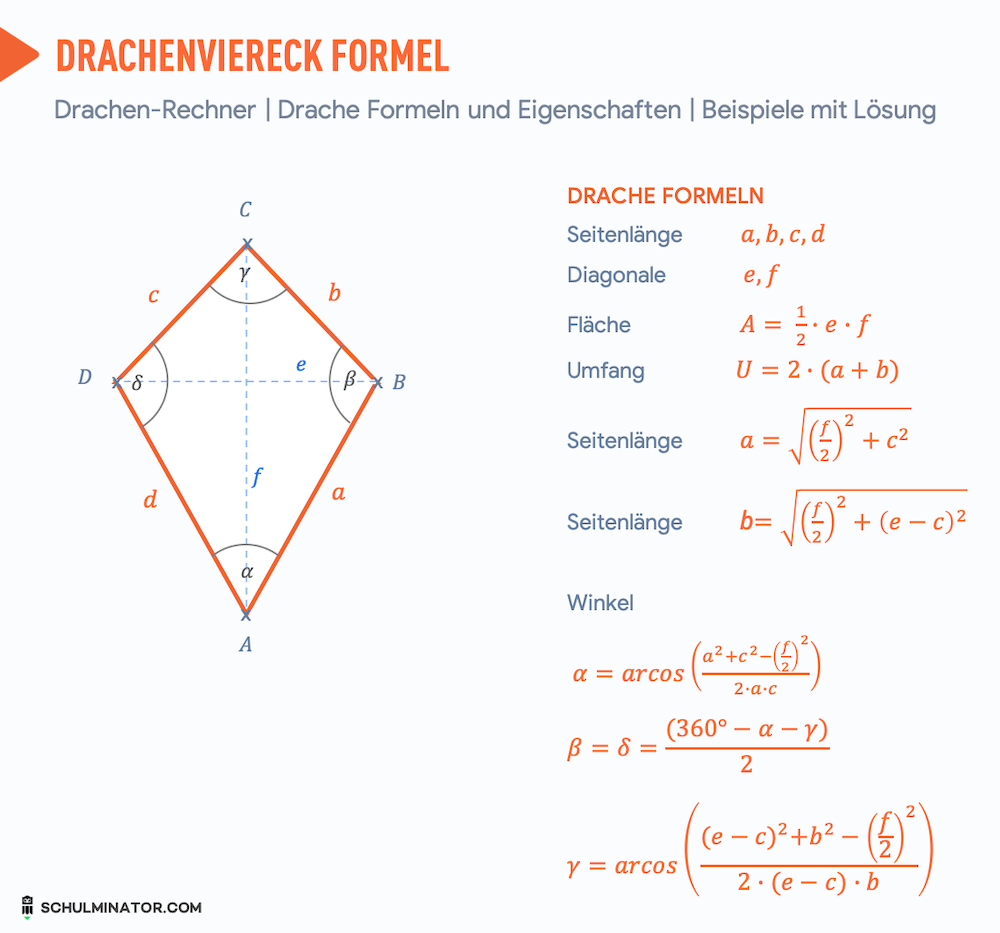
Drache Eigenschaften

  • Die Diagonalen $e$ und $f$ stehen senkrecht aufeinander.
  • Die Diagonale ff (längere Diagonale) bildet die Symmetrieachse des Drachen und halbiert die Diagonale $e$ und die Winkel. Die Diagonale $f$ halbiert auch den Drachen.
  • Die Diagonale $e$ (kürzere Diagonale) halbiert den Drachen in 2 gleichschenklige Dreiecke.
  • Die Winkel $\beta$ und $\delta$ sind gleich groß (liegen an der kürzeren Diagonalen).
  • Ein Drachenviereck hat immer einen Inkreis. Der Mittelpunkt des Kreises ist der Schnittpunkt der Winkelhalbierenden.
  • 2 Seiten sind paarweise gleich lang, liegen sich aber nicht gegenüber: $\overline{AB} = \overline{AD}$ und $\overline{CB} = \overline{CD}$.
Bild
Drache Formel
Erklärung

Drachenviereck Aufgaben mit Lösungen

1. Drachenviereck Umfang und Fläche berechnen

Berechne den Flächeninhalt und den Umfang für die folgenden Rauten:

a) $a = 4cm$, $b = 7 cm$, gesucht Fläche

b) $e = 2m$, $f = 5,5m$, gesucht Umfang

a) Für den Umfang gilt: $U = 2 \cdot (a + b)$.

Damit ist der Umfang $U = 2 \cdot (4 + 7) = 56cm$.

b) Für die Fläche gilt: $A = \frac{1}{2} \cdot e \cdot f$

Damit ist die Fläche $A = \frac{1}{2} \cdot 2  \cdot 5,5 = 5,5m^2$.

 

2. Drachenviereck Seiten berechnen

Von einem Drachen ist der Umfang und die Seitenlänge gegeben:

$U = 30m$, $a = 5m$

Berechne die Seitenlänge b. 

Die Formel für den Umfang $U = 2 \cdot (a + b)$ können wir nach b auflösen:

$b = \frac{U}{2} - a = \frac{30}{2} - 5 = 10m$.

 

3. Drachenviereck e und f berechnen (Diagonale)

Von einem Drachen ist der Flächeninhalt und eine Diagonalenlänge gegeben. 

$A = 50cm^2$, $e = 10cm$

Berechne die Diagonale $f$.

Für die Fläche gilt: $A = \frac{1}{2} \cdot e \cdot f$. 

Diese Formel stelle wir nach $f$ um:

$f = \frac{A \cdot 2}{e} = \frac{50 \cdot 2}{10} = 2,5cm$.

Wie hat dir dieses Lernmaterial gefallen?
Durchschnittliche Bewertung: 2.3 (Anzahl 26)

Kommentare